§ 6   Rowdang canonical form of square matrix

 

1. Invariant subspace

 

Let L be a linear transformation of a real (or complex) linear space V , and S be a subspace of V, if , then S is an invariant subspace about L.

Let be an invariant subspace of a linear transformation L of an n -dimensional linear space V , and V can use their direct sum:

The necessary and sufficient condition to represent is: the matrix A corresponding to the linear transformation L can be reduced to a block diagonal matrix under a certain basis

The order in the formula is equal to the dimension of .

 

Second, the standardization of the square matrix

 

The form of [ Ruodang block and Ruodang standard square matrix ]   is

The m -order square matrix of is called the Rodang block, where is an eigenvalue .

 The sub-matrix of a block matrix of a square matrix on the main diagonal is a block, and the rest of the sub-matrix are zero matrices, that is,

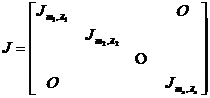                                              ( 1 )

Then it is called the Rowdang standard square matrix or the Rowdang standard form . Note that these are not necessarily different in different blocks .

[ Standardization of Square Matrix ]

1 ^{o In} the case of different eigenvalues ​​If the eigenvalues ​​of a square matrix A are not equal, then A can be transformed into a diagonal matrix, 

The elements on its main diagonal are these eigenvalues:
                                 

2 ^o When the eigenvalues ​​are equal, any square matrix A can be transformed into its similar Rowdang standard form ( 1 ), where 

is its eigenvalue and is the multiplicity of eigenvalues . If the order of the blocks is ignored, the canonical form of A is unique .

It can be reduced to a diagonal matrix if and only if the order of all the blocks is equal to 1. This is the case of 1 ^o .

As explained above, assuming that A is a square matrix, then a non-singular square matrix T can always be found , making the square matrix similar to A.
                             

 

3. Methods and steps of square matrix standardization

 

[ λ Matrix ]   Assuming that the elements of an n -order square matrix A are all complex coefficient polynomials of variable λ , it is called a λ matrix . The highest order r of a sub-form of a λ matrix that is not equal to zero is called the rank .
                    

    [ Invariant factor and elementary factor ]  Let r be the rank, k is a positive integer , and the highest common factor of all k -order sub-formulas of is a polynomial, and the specified coefficient of the highest-order term is 1 ; in addition, it is specified that

            

say

                       

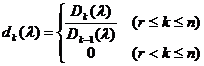
invariant factor for .

Decompose each into a first-order factor, we get

         

Some of the exponents in the formula may be zero, and at that time , it is called an elementary factor of .

    [ Elementary Transformation · Matrix Equivalence ]   A finite combination of the following three transformations on the λ matrix is ​​called an elementary transformation .

( i ) any two rows (columns) are interchanged;

( ii ) Multiply each element of any row (column) by the same λ polynomial and add it to the corresponding element of another row (column);

( iii ) Multiply any row (column) element by the same complex number not equal to zero .

It should be noted that, properly implementing ( ii ), ( iii ) both transformations can yield ( i ) .

If it can be obtained by a finite number of elementary transformations, it is said to be equivalent to .

After the λ matrix undergoes elementary transformation, its invariant factor and elementary factor remain unchanged .

[ Standard form of λ matrix ] Let the rank of the λ matrix be r and the invariant factor be , then 

              

Call the square matrix on the right the canonical form . It is determined by unique .

Equivalent λ matrices have the same canonical form .

[ eigenmatrix ]   The eigenmatrix of square matrix A is a special λ matrix . So

1 ^o If the elementary factor is

                  

which are not necessarily different from each other, then

                    

and have

      

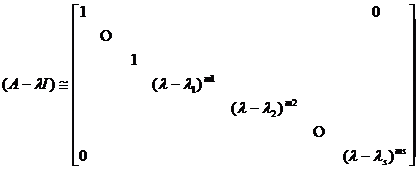
    2 ^o if the nth order λ matrix

              

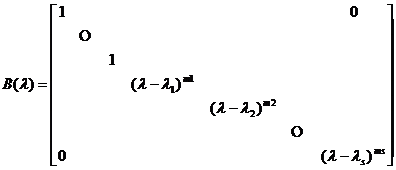
Among them , then

where J is the standard form of A.

3 ^o If the elementary factor of the characteristic matrix of A is

           

but                             

If J is the standard form of A.

    [ Steps of Square Matrix Standardization ] The steps   to convert the square matrix A into the standard form of A are as follows:

    (1)  Use elementary transformation to convert it into a diagonal matrix, decompose the polynomial on the diagonal, and get all the elementary factors .

(2)   Corresponding to each elementary factor , make a m -order Row-Dang block
                    

    (3)   Combine all the Ruodang blocks to get the Ruodang canonical form of A.

    Example 1 to   find a square matrix        

         

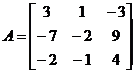
The Jodang standard form of .

    untie

                   

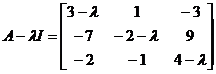
It is easy to find that its invariant factors are 1 , 1 , , so the elementary factors are

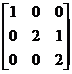
    Example 2   Find a square matrix

                          

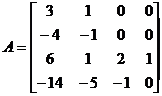
The Jodang standard form of .

untie   

                   

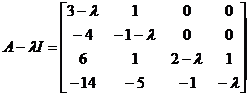
After elementary transformation, it can be transformed into a diagonal matrix of the following form

                           

So the elementary factor is , , and the corresponding if-dang block is

Therefore , the standard form of A 's jodang is